Hunting for Exoplanets
A team of exoplanet searchers recently released a large set of data. The goal of this article is to review one method of finding exoplanets, and then to apply those methods to the released data.
Background
When solving for planetary orbits, most students are told to make the simplifying assumption that the star is infinitely massive. However, the star really does have finite mass and mutually orbits its planets. This motion would appear to the observer as a periodic wobble in the velocity of the star. We should be able to detect this stellar wobble, and thus infer the existence of an exoplanet.
Systemic
Systemic Console 2 is a tool for analyzing stellar velocity data for the presence of exoplanets. It comes pre-loaded with radial velocity data from many sources. There is a 4 part tutorial on using the software. Though it is written for an older version, the core features are the same.
Unfortunately, I ran into several problems trying to get Systemic Console 2 to work properly. On my Mac laptop, I ran into a launch time problem, and found the corresponding github issue. I then installed an Ubunutu 16.04 virtual machine and attempted to run the software in that environment. The results were more promising (the application opened), but ultimately unsuccessful. A quick search revealed that I am not alone and that an issue had already been reported.
Fortunately, there is also a web-based version of Systemic called Systemic Live. I can load the HD 4208 data into the program just like in the tutorial.
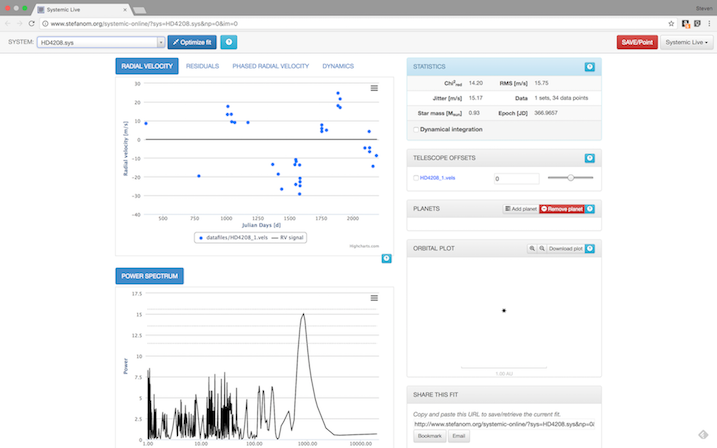
Manually adjusting the parameters and then applying the optimization yields the following fit.
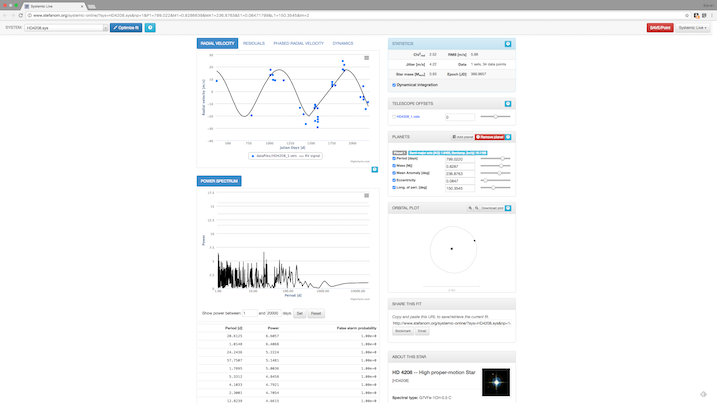
With a χ2 = 2.52, the fit here isn’t as good as the one in the desktop version of the tutorial. Starting from different manual adjustments reaches different fits, but this was the best one I achieved.
Manually fitting the data
Since I couldn’t get Systemic Console to work properly and Systemic Live doesn’t allow data sets to be uploaded, I made an attempt to write my own curve-fitting techniques. We will take a look at the same star as above, HD 4208. First, we inspect the data file from the Keck data set.
2451010.10523 17.69 1.20 0.1653 -1.00000 118398 275
2451014.09906 16.36 1.57 0.1549 -1.00000 108803 220
2451043.04968 17.16 1.36 0.1620 -1.00000 153146 300
2451044.03377 14.95 1.54 0.1695 -1.00000 123400 250
2451068.93885 17.62 1.45 0.1666 -1.00000 112870 350
2451172.74280 11.17 1.21 0.1724 -1.00000 103587 330
2451368.07957 -11.41 1.33 0.1621 -1.00000 83174 170
2451412.06450 -9.44 1.43 0.1679 -1.00000 81332 200
2451543.73889 -16.59 1.42 0.1603 -1.00000 70334 300
2451550.72615 -13.45 1.38 0.1653 -1.00000 70202 246
2451551.71323 -15.73 1.38 0.1610 -1.00000 62811 300
2451552.71126 -19.21 1.29 0.1614 -1.00000 76306 400
2451580.70569 -15.87 1.52 0.1592 -1.00000 69841 240
2451581.70668 -20.39 1.50 0.1615 -1.00000 54075 220
2451582.72443 -22.11 1.49 0.1784 -1.00000 53935 210
2451583.70664 -18.30 1.58 0.1711 -1.00000 54115 240
2451585.70754 -15.08 1.58 0.1708 -1.00000 51083 300
2451755.03303 14.05 1.28 0.1882 -1.00000 88457 500
2451756.02566 9.54 1.38 0.1874 -1.00000 82038 500
2451757.07363 10.84 1.24 0.1723 -1.00000 92138 500
2451793.93004 9.57 1.45 0.1871 -1.00000 68418 241
2451882.72859 21.83 1.28 0.1563 -1.00000 77493 240
2451883.77274 20.19 1.41 0.1628 -1.00000 76855 248
2451899.77756 21.60 1.11 0.1661 -1.00000 99607 421
2451900.74929 14.63 1.30 0.1603 -1.00000 93264 258
2452095.11183 3.92 1.68 0.1309 -1.00000 98288 273
2452129.09608 0.00 1.46 0.1450 -1.00000 84005 197
2452133.04676 -4.75 1.49 0.1405 -1.00000 76686 145
2452134.00916 -4.97 1.43 0.1477 -1.00000 81811 150
2452161.92847 -10.02 1.56 0.1499 -1.00000 81097 176
2452187.98133 -8.49 1.48 0.1476 -1.00000 80402 475
2452489.03795 -2.16 1.64 0.1509 -1.00000 91243 148
2452538.89542 4.94 1.67 0.1498 -1.00000 97016 161
2452601.80071 8.16 1.49 0.1534 -1.00000 111846 275
2452833.08079 15.11 1.62 0.1401 -1.00000 97009 166
2453196.07518 -20.63 1.72 0.1428 -1.00000 98598 150
2453604.08199 17.84 1.39 0.1432 0.03119 103305 184
2454464.81619 7.83 1.41 0.1699 0.03083 71875 0
2455169.84484 9.33 1.39 0.1672 0.03125 50867 141
2455169.84730 5.34 1.36 0.1637 0.03127 47470 136
2455467.04618 -18.28 1.36 0.1535 0.03115 49407 107
2455807.09469 -17.88 1.52 0.1485 0.03123 49077 152
2456138.13949 0.95 1.38 0.1489 0.03102 47374 81
2456513.13532 -39.46 1.59 0.1578 0.03112 49372 80
2456613.86212 -24.23 1.32 0.1578 0.03134 48670 92
2456638.73076 -15.93 1.46 0.1592 0.03126 50469 121
2456874.13410 -1.28 1.51 0.1509 0.03106 48822 101
2456907.08927 -0.43 1.59 0.1567 0.03121 49106 93The first column is the Julian Date. The second column is the measured velocity in m/s. The third column is the uncertainty in the velocity, also in m/s. The fourth column is the S_value and the fifth column is H_alpha. The fifth column is the median number of photons per pixel, and the fifth column is the exposure time in seconds.
References and Links
- Butler, Vogt, Laughlin, et al., The LCES HIRES/KECK Precision Radial Velocity Exoplanet Survey (2017) Link
- Data release
- Systemic Console homepage
- Systemic Console on Github
- 4 part Systemic Console Tutorial